Of Vertices and Symmetry: Part Two

The original document is an OpenOffice .odt file. There is no guarantee that any other format properly preserves or displays the higher valued unicode characters used in this document.

I continued to play with symmetric functions and decided to approach things more systematically. Symmetric functions are symmetric about x = 0, any x-intercept on the negative x-axis is mirrored by an x-intercept on the positive x-axis.

Even functions have a minimum or maximum at x = 0 and odd functions have a zero at x = 0.

The functions are built up from the multiplication of linear factors of the form (x ± r_n). The result is a lead coefficient of 1. Linear factors of the form (ax ± b) can be converted to the earlier form by dividing through by a, thus preserving the lead coefficient of one.

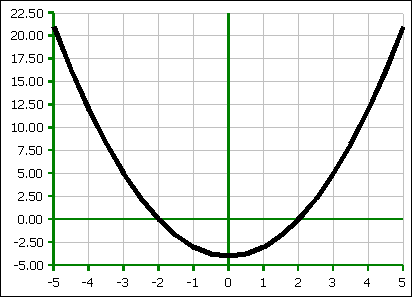
Symmetric Quadratic Functions

Symmetric quadratic functions with real x-intercepts have the form f(x) = x² − r² with factors (x + r)(x − r) and solutions at x = ±r. The minimum (or maximum if f(x) = − x² + r² ) is at 2x = 0 or x = 0. There is no second derivative and hence no inflection points.

Symmetric Cubic Functions

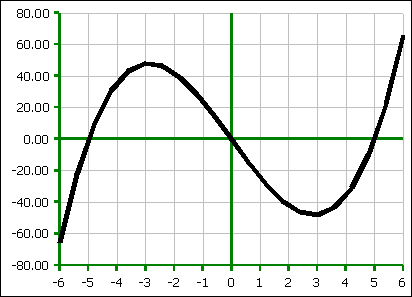
Symmetric cubic functions with real x-intercepts have the form f(x) = x³ − r²x with factors x(x + r)(x − r) and solutions at x = 0, ±r.

If the functional form is f(x) = x³ + cx then the solutions would be at 0, ±√c.

The x-values for the minimum and maximum are found by setting the first derivative equal to zero: 3x² − r² = 0. Solving for r reveals:

From the second derivative, the inflection point is at 6x = 0 or x =0.

Bearing in mind that this work derives out of teaching algebra, and the penchant for instructors to pick integer values for r, the minimum and maximum will always be irrational.

This has one subtle impact. When students graph cubics, they typically calculate values of f(x) for integer values of x only and then "connect the dots" and presume the minimum and maximum of their graphs are at an integer value of x.

For some values of r, the connect the dots approach also often leads to the impression that the minimum and maximum are symmetric about the minimum and maximum with the minimum and maximum at the midway point between ± r and the x-axis. This is not the case, the minimum and maximum are always "pushed outwards" slightly from the ±r/2 midpoint.

The "outward push" is by an amount that is the difference of r√3/3 and r/2 or 0.5774r and 0.5r. This represents a difference of about 15% between the r/2 midpoint and the location of the minimum and maximum.

Symmetric Fourth Order Functions

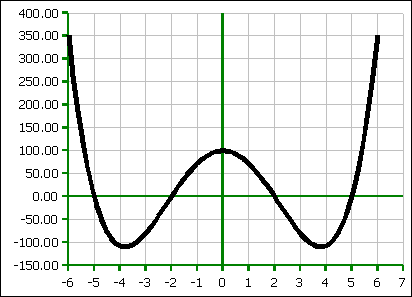
For x-intercepts at ±p and ±q, the above function is built up from:

f(x) = (x+p)(x+q)(x−p)(x−q) = ( x² − p²)( x² − q²) = x⁴ − ( p² + q²)x² + p²q²

Thus symmetric fourth order functions always have the form f(x) = x⁴ + c x² + e. This form is soluble by substitution.

Although an odd thing to do, if one solves x⁴ − ( p² + q²)x² + p²q² by substituting n = x² and completing the square for the quadratic in n, one obtains the following result for the x-intercepts:

This can be shown to degenerate back to simply ±p and ±q.

If one faces the form f(x) = x⁴ + c x² + e, then the same substitution yields f(x) = n² + c x + e and once again completing the square will solve this equation as well:

x =

Not unlike a fancy quadratic formula. I usually actually avoid teaching the quadratic formula as completing the square is the more useful tool to have in the toolbox. I have found that memorizing a mathematical process is far more productive than memorizing a formula.

The central maximum is at x = 0 and has a height equal to p²q², this is useful to know when one is building a quiz or test and wants an idea of the scale that will be necessary on the y-axis. The minimum and maximum, however, may be more extreme than the central peak. This depends on the choice of p and q.

The minimum and maximum are found from 4x³ − 2( p² + q²)x = 0. The minimum and maximum are thus at x = 0 and at:

Plugging the above into the original function yields a height of the mountain and depth of the valley to be:

Thus there are values for which the height and depth will be integers values – a fact of esoteric interest only to algebra teachers if even them.

There are two inflection points at:

Symmetric Fifth Order Functions

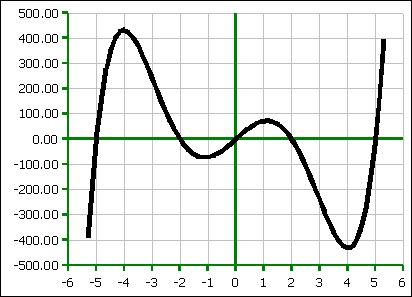
The symmetric fifth order function reveals more clearly the developing asymmetry in the shapes of the mountains and valleys that form the maxima and minima. Equations with x-intercepts at 0, ±p, and ±q have the functional form:

f(x) = x⁵ − ( p² + q²)x³ + p²q²x

These functions, in general of the form f(x) = x⁵ + cx³ + ex can be reduced back to their fourth order counterpart by dividing out by x. The equation can then be solved by substituting n = x² and completing the square in n. Any equation of the form c = − ( p² + q²) and e = p²q² will be a nicely symmetric fifth order function, thus building such equations is fairly easy.

I have not worked further with these functions. Bear in mind from the first paper that functions which might resemble the head of Batman against the night sky were those of most interest to me and to my sidekick Marlin.

Symmetric Sixth Order Functions

In the previous paper I had explored a special case where two of x-intercepts of a sixth order function were degenerate, that is, where a symmetrical pair of minima just touched the x-axis. At the time I had considered the general sixth order symmetric function to be too complex.

While the general sixth order symmetric function is not soluble by trivial methods (the substitution n = x² yields a cubic equation), the minima and maxima locations turn out to be soluble.

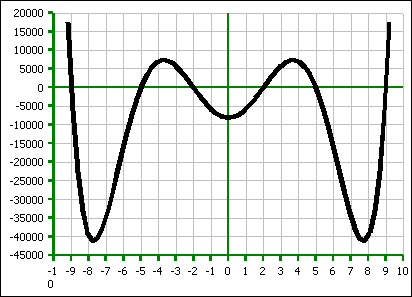
The above, while not Batman against the night sky, can be imagined to be a bat hanging from the ceiling of a cave, with its wings extending down past its head. The function has the general form, and here I was working with x-intercepts at ±a, ±b, and ±c:

f(x) = x⁶ − (a²+b²+c²) x⁴ + (a²b²+a²c²+b²c²)x² − a²b²c²

While the above, when in the form f(x) = x⁶ + gx⁴ + hx² +k is not trivially soluble, the first derivative has a removable zero at x = 0:

f'(x) = 6x⁵ − 4(a²+b²+c²) x³ + 2(a²b²+a²c²+b²c²)x = 0

6x⁴ − 4(a²+b²+c²) x² + 2(a²b²+a²c²+b²c²) = 0

Let n=x² and the equation 6n² − 4(a²+b²+c²)n + 2(a²b²+a²c²+b²c²) = 0 can be solved by completing the square. Many pages of algebra I obtained:

The result was quite pleasing and I was left wondering if the eighth degree function would have minima and maxima at some location

I did not try to chase this, even the insane know insanity.

I did eventually play with eighth degree quadruple touch functions that have four minima on the x-axis. In this case four x-intercepts can be divided out – they are known – using long division. Likewise, the first derivative can be reduced from a seventh order equation to a sixth order by taking out the maximum at x = 0 and then dividing out the four minima with long division. The result should be a quadratic or symmetric fourth order which could be solved similar to above cases.

Performing the above using arbitrary roots such as ±a, ±b, ±c, ±d, bogged me down in horrendous piles of algebra. I realized I needed a math software system such as LiveMath or Mathematica to handle the long division. I also looked at a tenth degree quadruple touch function, but it too was horribly complex.

I returned to the sixth order equation and played with what happens when the x-intercepts multiply to one in an attempt to control the extreme values such functions tend to generate.

I also chased the second derivative, but the surf came up and I took to exploring oceanic sine waves and Fourier series instead. After all, I already had all of the shortcuts I needed for drawing bat functions for Marlin.

Dana Lee Ling

05 August 2005