This function is actually a symmetrical function with x-intercepts at ±1, ±2, ±3. I was playing with a variant of the above function, f(x) = x6 − 54x4 + 825x2 − 2500
Of vertices and symmetry
The original document is an OpenOffice .odt file. There is no guarantee that any other format properly preserves or displays the higher valued unicode characters used in this document.
Teaching MS 100 College Algebra has me once again playing with polynomials. I was playing with functions that make shapes akin to the outline of Batman's head against the moon. Marlin loves Batman, so he likes the graphs that some of these generate. The function:
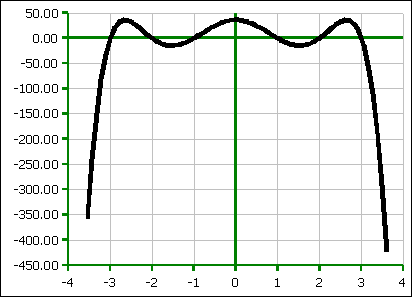
f(x) = −(x6 − 14x4 + 49x2 − 36) generates the graph:

This
function is actually a symmetrical function with x-intercepts at ±1,
±2, ±3. I was
playing with a variant of the above function, f(x) = x6 −
54x4 + 825x2 − 2500
which looks like:
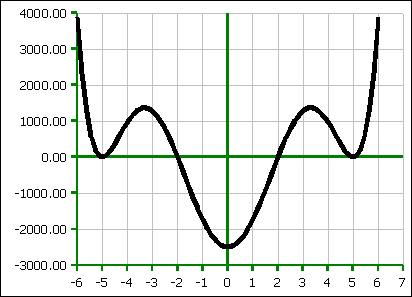
As
I started playing with this function, with x-intercepts at ±2,
±5, ±5 (no mistake: there is a double root at ±5,
creating the “touch and go” at ±5 on the x-axis),
I realized that I could actually calculate all of the local minima
and maxima for the function because three of the five were
predetermined and the other two were soluble by completing the
square.
The first derivative f'(x) = 6x5 − 216x3 + 1650x and to find the local minima and maxima:
6x5 − 216x3 + 1650x = 0
Thus x = 0 is a solution, as expected, and there is a minima at that location. Dividing out by x reduces the equation to a fourth power equation, but the symmetry of the x-intercepts provides a way to analytically solve the remaining “reduced” equation:
6x4 − 216x2 + 1650 = 0
Let n = x2 and then solve 6n2 − 216n + 1650 = 0 by completing the square. When the dust has settled one is left with:
![]()
I have left the radicals in place because while researching the formula for analytic solutions to cubic equations I had noted formulas with “nested” radicals and wondered why they arose. The result is solutions at ±5 and ±√11. The former were expected – the function was constructed to have those minima, and the later are now the exact solutions to the inner two local maxima.
At about this time my students were wrestling with vertices for parabolas. The vertex for f(x) = ax2 + bx + c occurs at − b/(2a). This is also the axis of symmetry and the value of h in (y − k) = a(x − h)2. Substituting h into the function generates k.
I realized that the vertex is actually nothing other than the first derivative, but we cannot tell the MS 100 students this because they do not yet know calculus. The formula for the vertex, however, is no more mysterious to them than the process for finding a simple derivative. We make calculus more complex by proving our formula works using the difference formula [f(x+h)-f(x)]/h and thus obscure a perfectly good memorizable tool: the derivative of axn is naxn-1
Be that complaint as it may, I became intrigued by a thought that has always puzzled me: why do we quit talking about useful concepts as we move up through the polynomials? That is, once one hits quadratics we suddenly stop talking about y-intercepts. Yet they still exist. Once we hit cubics we suddenly stop talking about vertices. Yet they have two vertices, and they can always be solved for: the first derivative of a cubic is a quadratic and that can be solved by completing the square.
We teach a lot of tips and tricks to get better graphs of polynomials in chapter three of the current text, but the really important features are the minima, maxima, and inflection points. And only calculus gets at those. And for functions like the “bat” functions, there is always a central symmetry point about which the numbers “repeat.” This is a useful feature when one is using a hand calculator at home. For these functions, whether even or odd, there is either an origin symmetry or a y-axis symmetry that can be used to cut one's hand calculations in half.
I began to think about how one calculates features in functions such as f(x) = x6 − 54x4 + 825x2 − 2500 during a long final. I started by calling the outer x-intercepts as being ±a and the inner intercepts as being ±b. I then multiplied (x+a)(x−a)(x+a)(x−a)(x+b)(x−b) to get f(x) = x6 − (b²+2a²)x4 + (2a²b²+a4)x2 − a4b²
I took the first derivative and then divided out by the common x term (that is the central minima). I did the following long division on the result:
(6x4 − 4(b²+2a²)x²+ 2(2a²b²+a4)) ÷ (x² − a²)
Part way through a couple pages of algebra I found a mistake and tried again. By later that evening I was surrounded by paper. I shouted with joy when all of sudden the result simplified rather wonderfully. My family simply looked at me and shook their heads figuring I was delusional. I did, however, have a result. The local maxima are, if I did not botch my calculations, are at:
![]()
I then decided to chase the inflection points, as I had done for f(x) = x6 − 54x4 + 825x2 − 2500.
After even more pages of paper I had:
![]()
I decided not to even check whether that held true. I was only amazed that the inflections for a sixth order function could be expressed using square roots, I somehow expected sixth roots or something like that. Still, the tail end of the above is technically a fourth root.
I think the above also encapsulates for me what it means to be algebraically “literate.” A student has learned to algebra when they can fully explore a function such as f(x) = x6 − 54x4 + 825x2 − 2500 and can handle purely abstract symbolic manipulations of equations such as f(x) = x6 − (b²+2a²)x4 + (2a²b²+a4)x2 − a4b²
If a student can “play” with and explore functions, that is algebraic literacy. This is the prose and poetry of algebra. Not the drill and practice in the textbook. Not adding fractions with unlike denominators. And not “math skills for the workplace.” The current textbook is riddled with “how this is used in the workplace” examples. Baloney. This is no more used in the work place than poetry. And of course someone somewhere is using poetry in the workplace, just like someone somewhere is using algebra. The vast bulk of humanity gets by in their day-to-day existence without ever doing a lick of algebra. One does algebra for the same reason one studies poetry: there is a philosophical beauty underneath algebra. Truisms that are provable true, surety in a solution. In math there is that most elusive of ethereal qualities, there is truth.
I wandered out into the mosquito infested taro swamp behind the house and returned to the issue of the central point of symmetry and realized that for a function of degree n, the n − 1 derivative, the "last" derivative one can take, is probably the point of symmetry. For a quadratic the "nth but one" or n − 1 derivative is equal to 2 − 1 = 1 so the first derivative set equal to zero is the symmetry point. And this is most obviously true:
For f(x) = ax2 + bx + c
f'(x) = 2ax + b
And the vertex x, the axis of symmetry, is 2ax + b = 0 or x = −b/(2a)
One can check that the second derivative of a cubic is the central symmetry point, noting as always that I am limiting my comments to functions whose x-intercepts are symmetric about the y-axis. If a function is not symmetric about the y-axis, then translate it horizontally and/or vertically until it is symmetric. Thus the only remaining constraint I am imposing for degree > 2 is the the function have a point at which the x-intercepts are “evenly” spaced.
Returning to the fn− 1(x) derivative where n is the degree of the equation, a little time in a taro swamp will cause one to realize that all terms where the power of x is n − 2 or lower are lost.
Now for functions of the form (x+p)(x+q)(x+r)... the lead two terms are xn + (p + q + r + ...)xn− 1 + ....
The lead two terms can be written as:
axn + bxn− 1
where b = (p + q + r...). Note that a =1 for the functions this paper examines. A function where a ≠ 1 can be divided through by "a" in resulting in a lead term coefficient of one.
In the above situation fn− 1(x) = 0 should yield something like:
![]() or
or
![]() for
the central symmetry point. Note that for even symmetric functions b
is the coefficient on the term that is one less than the degree of
the term. This is an odd term and does not appear in an even
function. A second paper, since written, go into this in more
detail.
for
the central symmetry point. Note that for even symmetric functions b
is the coefficient on the term that is one less than the degree of
the term. This is an odd term and does not appear in an even
function. A second paper, since written, go into this in more
detail.
I
haven't a clue as to how to prove that
![]() is
always the central axis of symmetry. It made sense when I was in the
taro patch. To assert it works for n = 2 and n = 3 proves absolutely
nothing, but I felt satisfied. Which is why I never made it any
further than I did in mathematics. Once I had a probable result, I
never wanted to do the hard work to show that my probable result
would hold for all cases.
is
always the central axis of symmetry. It made sense when I was in the
taro patch. To assert it works for n = 2 and n = 3 proves absolutely
nothing, but I felt satisfied. Which is why I never made it any
further than I did in mathematics. Once I had a probable result, I
never wanted to do the hard work to show that my probable result
would hold for all cases.
After all, I was only going for shortcuts to drawing bat functions for Marlin.
Dana Lee Ling
20 July 2005