1. Find the center (h, k) and radius of the circle (x − 6)² + (y - 9)² = 36

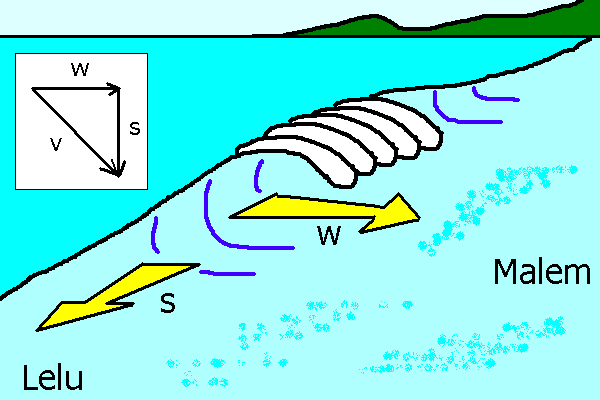2. On Thursday evening I was body board surfing in Malem. My total velocity v (speed) was the result of the vector addition of the velocity (speed) of the wave w and the velocity (speed) of my board along the face of the wave. The equation is:
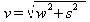
On Thursday the waves were moving at a speed of
w = 3.9 m/s towards Malem and my board was moving at
s = 4.1 m/s towards Lelu. Use the equation given to calculate my total velocity v.

3. For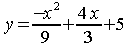

a. Find the y-intercept.

b. Find the x-intercepts (zeros) by completing the square.

4. Multiply the following complex conjugates: (6 + 9i)(6 − 9i)

5. For

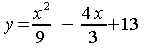
a. Find the y-intercept.
b. Find the x-intercepts, whether real or complex.

8. Solve the inequality and sketch the solution on a number line:

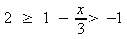
9 a. Find the equation of the line through (4, 3) and ( − 2, 12)

b. Is y = 1.5x + 54 parallel, perpendicular, or neither to the line in 9a?
c. Is y = − 1.5x + 54 parallel, perpendicular, or neither to the line in 9a?

10. A yard of silk fabric is marked up from $6.00 per yard to $9.00 per yard. What is the percentage difference?

11. Perform the long division (x³ − 18x² + 27x + 270) ÷ ( x − 15)

12. For f(x) = 6x + 9 and g(x) = 9x − 6 find

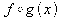
13. For f(x) = 9x − 6 find 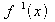using

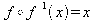
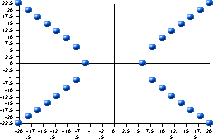
14. What is the name of the shape seen in this graph:

15. For the equation:

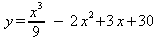
a. Find the y-intercept.

b. Given that partial factorization of the above is (1/9)( x − 15)(x² − 3x − 18), find all of the x-intercepts (zeros).

c. Is the lead coefficient positive or negative?

d. Is an even or odd function?

e. Complete the square for 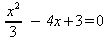to find the x-values for the local maximum and minimum.

f. Find the axis of symmetry for 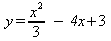(The axis of symmetry of that equation is the x-value of the inflection point of )

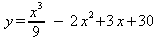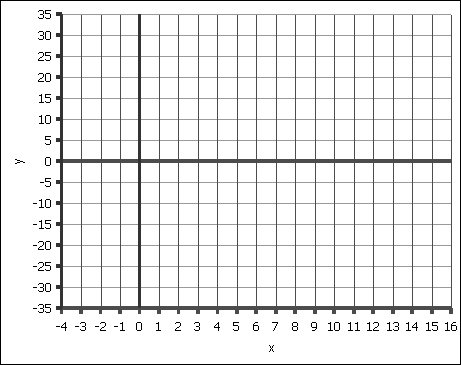
g. Use the above information to roughly sketch a crude but somewhat accurate graph of the function without calculating every single value along the x axis.

h. Does the equation pass the vertical line test?

i. Is the equation a function?

j. Does the equation pass the horizontal line test?

k. Is the inverse of the equation also a function?

l. Does the graph have x-axis symmetry, y-axis symmetry, origin symmetry, or no symmetry?

m. Is the graph symmetric about any line? If so, what line?

n. Mark the increasing and decreasing intervals on the graph.

o. Mark the sections of positive and negative curvature on the graph.

p. Mark the local minimum and maximums on the graph.

q. Mark the inflection point.