Illustration
1: Frequency Distribution
COMET Admissions Examination Statistical Summaries Spring 2008
09 June 2008 Notes: This document should be taken as draft work in progress. Consider these results to be preliminary and subject to revision and correction at a later date.
In this statistical summary those who took the College of Micronesia-FSM Entrance Test (COMET) are referred to interchangeably as "students" and "candidates." There is no distinction intended by these two terms.
Basic Statistics
The COMET admissions examination consisted of four main sections. The four main sections included an essay, vocabulary, comprehension, and a math section consisting of four subsections. The basic statistics for these sections and subsections are presented in the table one below.
|
Statistic |
Essay |
Voc |
Comp |
95 |
96 |
99 |
100 |
msum |
COMET |
|
count |
1601 |
1607 |
1607 |
1536 |
1536 |
1536 |
1536 |
1614 |
1614 |
|
min |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.00 |
|
max |
50 |
43 |
47 |
10 |
10 |
10 |
9 |
38 |
1225.7 |
|
range |
50 |
43 |
47 |
10 |
10 |
10 |
9 |
38 |
1225.8 |
|
midrange |
25 |
21.5 |
23.5 |
5 |
5 |
5 |
4.5 |
19 |
612.8 |
|
mode |
0 |
10 |
14 |
7 |
3 |
2 |
2 |
15 |
- |
|
median |
25 |
11 |
17 |
7 |
4 |
3 |
2 |
16 |
541.38 |
|
mean |
24.35 |
12.35 |
18.52 |
6.83 |
4.6 |
3.6 |
2.55 |
17.5 |
552.38 |
|
stand deviation |
12.82 |
6.26 |
7.55 |
2.19 |
2.53 |
2.18 |
1.59 |
6.44 |
221.74 |
|
coef variation |
0.53 |
0.51 |
0.41 |
0.32 |
0.55 |
0.61 |
0.62 |
0.37 |
0.40 |
Table 1: Basic statistics
Essay is the essay score out of 50.
Voc is the vocabulary score out of 45.
Comp is comprehension out of 48.
95 is the first math subsection and contains ten arithmetic level problems.
96 is the second math subsection and contains ten prealgebra level problems.
99 is the third math subsection and contains ten elementary algebra problems.
100 is the fourth math subsection and contains ten college level algebra problems.
msum is the sum of the math subsections and is out of forty.
Correlations
Although the first two subsections of the math test were rewritten in 2006 to require less reading ability, the math sum remains, given the sample size, correlated moderately to the essay and comprehension sections of the examination.
|
|
Essay |
Vocabulary |
Comprehension |
math sum |
|
Essay |
1.00 |
0.53 |
0.62 |
0.55 |
|
Vocabulary |
0.53 |
1.00 |
0.72 |
0.52 |
|
Comprehension |
0.62 |
0.72 |
1.00 |
0.60 |
|
math sum |
0.55 |
0.52 |
0.60 |
1.00 |
|
z-score |
0.92 |
0.75 |
0.82 |
0.74 |
Table 2: Correlations
At present the college seeks to admit 400 students into associates degree programs. The college accepts the top 400 students into associates degree programs. The rank order is generated by a sum of z-scores detailed later in this report. The 0.92 correlation for the essay to the z-score reflects the 50% weight of the essay score in the z-score. The rank order is supposed to be strongly correlated to the essay performance by design. The results above support that this goal was achieved.
The moderate correlation for mathematics indicates that mathematics is linked to language skills, at the same time the mathematics score provides independent information on the abilities of the candidate. Thus the mathematics score is valuable for a more comprehensive picture of the skills the candidate possesses.
The question is often asked, would student "x" have been admitted if their math score was stronger. In other words, does the math section keep students from attaining associates degree admission. The above correlations should provide statistical assurance that the math section alone did not "sink" a student – the essay was the strongest driver of the rank order. In addition, there is a correlation between math and English, so a really weak math score for a given set of language scores may suggest the student is weaker than the language test results indicate. Again, the mathematics score is important to providing a broader picture of the student's academic abilities.
Distributions
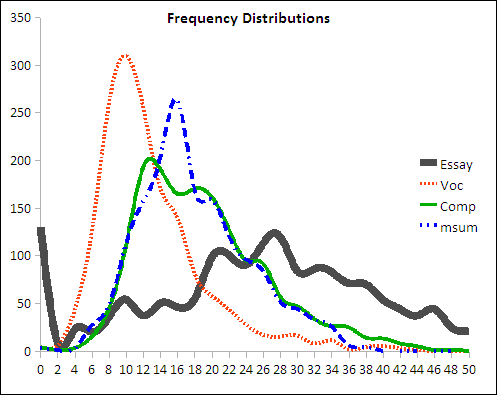
The distribution of scores on each section is given in illustration one. The score is on the horizontal axis, the vertical axis is the number of students with that score.

Illustration
1: Frequency Distribution
With the exception of the writing section, the other sections distributed in a manner which is considered statistically reasonable. That is, the frequency (the number of students) rises with the score towards the mean, and then falls as the score continues to rise past the mean to the maximum possible score. If the distribution (the shape of the curve) is a symmetrical heap, the most common score is also the mean score as well as the median score. This distribution is sometimes called a "bell curve" and is mathematically described by the normal or student's t-distribution.
In the past, the writing section, the essay, has in performed in a statistically reasonable fashion except for the number of students who score a sum of zero. This was true again this year with 130 scores of zero. In the spring of 2006 there were 235 scores of zero for 1783 candidates (13%). In the spring of 2007 there were 144 scores of zero for 1608 candidates (9%). Spring 2008 there were 130 scores of zero for 1601 candidates (8.1%). This suggests that the percent of students scoring zero is declining.
In the spring of 2006, the most common score on the essay, except for zero, was the then maximum possible score of 40. There was anecdotal evidence that the rubric needed to be adjusted as papers that varied in quality were "maxing out" at 40. A change in the rubric permitted a maximum score of 50 in 2007. In both 2007 and the current run of the test, the right tail of the essay distribution now falls steadily from the mean to the maximum possible. With the adjustment in the maximum possible in 2006, the essay continues to behave in a statistically reasonable manner.
Graders did raise questions on whether individual essay prompts behaved in a statistically equivalent manner. The lack of machine coding of the essay prompts and scores precluded analyzing the performance of individual prompts.
Year-to-Year Mean Scores by Section
The following table provides the mean score by entrance test subsection. Note that use of the reading section was discontinued in 2006. The grammar section was discontinued in 2007. A vocabulary and comprehension section based on the Gates-MacGinitie Level AR reading tests was added in 2008. The essay section was worth only 40 points in 2006, in 2007 and 2008 the essay section was worth 50 points.
|
Section |
2006 |
Section |
2007 |
Section |
2008 |
|
Reading |
14.81 |
|
|
|
|
|
Grammar |
37.04 |
Grammar |
34.87 |
|
|
|
Essay (40) |
20.69 |
Essay (50) |
22.03 |
Essay (50) |
24.35 |
|
|
|
|
|
Vocabulary |
12.35 |
|
|
|
|
|
Comprehension |
18.52 |
|
Math subsection one |
6.69 |
m1 |
6.63 |
m1 |
6.83 |
|
Math subsection two |
3.69 |
m2 |
4.04 |
m2 |
4.60 |
|
Math subsection three |
3.51 |
m3 |
3.40 |
m3 |
3.60 |
|
Math subsection four |
2.43 |
m4 |
2.49 |
m4 |
2.55 |
|
Math sum |
16.21 |
Math sum |
16.44 |
Math sum |
17.50 |
|
COMET |
544.34 |
COMET |
547.98 |
COMET |
552.38 |
Table 3: Year-to-year mean performance by section
The essay and math subsection scores suggest that the mean performance is improving. The improvements seen could be due to improved educational processes or better specific preparation for the COMET. In either case the COMET could be seen as a curricular impetus. The college might consider broadening the content scope of the COMET to provide an impetus for schools to improve in areas beyond English and Mathematics. The natural and social sciences are areas that might be explored for content oriented sections of the COMET.
Rank order and Program Placement
The admissions board approved a rank-order formula using z-scores. In spring 2008 the formula placed a 50% weight on the essay, 16.7% weight on vocabulary, 16.7% weight on comprehension, and a 16.7% weight on mathematics. The individual weighted z-scores were added to generate a sum of z-scores. The resulting z-score was linearly transformed to produced the final COMET score.
A COMET score of 700 was approved as the cut-off for regular admission to an associate degree program. A COMET score of 300 was established as the minimum score for admission to a certificate program. Students who have scored between 300 and 700 will be eligible to enroll in a certificate program.
Bear in mind that the college now operates based on fixed resources and specific projections of the number students that the college can serve. Each site has an target enrollment number and an maximum enrollment capacity limit. Like many smaller colleges, the college opts to admit a specific number of students.
The result is that the target admissions number is a fixed number. Put another way, there is not the possibility at present of all high schools increasing the number of students attaining regular admission to the college. If one high school sees an increase in the number of students who have attained regular admission, then some other high school (or high schools) must have seen a decrease in the number of students who gained regular admission. Thus admission is competitive and is mathematically termed a zero-sum game.
High schools that are using increases in regular admissions as an indicator do so at their own peril. If another high school improves by a larger amount, then that first high school could see a drop in admissions despite real improvement in their own educational processes. The college does not recommend using the entrance test as an performance indicator. The entrance test is designed solely for the internal admissions purposes of the college. That said, school that still choose to use the entrance test as a performance measure should look at improving average performance by section. This data is reported later in this report.
The next table records the distribution by state and high school of the students into the three categories delineated above.
|
School |
Non-admit |
Certificate |
Associates |
Sum |
|
Berea |
2 |
16 |
8 |
26 |
|
CCA PNI |
|
1 |
11 |
12 |
|
Chuuk HS |
39 |
68 |
7 |
114 |
|
CSC |
14 |
124 |
6 |
144 |
|
Chuuk SDA |
|
6 |
2 |
8 |
|
Faichuuk HS |
37 |
8 |
|
45 |
|
KHS |
6 |
95 |
47 |
148 |
|
KHS a1 |
|
|
21 |
21 |
|
KHS a2 |
|
10 |
12 |
22 |
|
Mizpah CHS |
4 |
13 |
3 |
20 |
|
Madolehnihmw HS |
7 |
73 |
20 |
100 |
|
Mortlocks |
13 |
17 |
|
30 |
|
Neighboring Island Central HS |
10 |
30 |
2 |
42 |
|
Nanpei Memorial HS all sect |
1 |
74 |
21 |
96 |
|
NMHS a1 |
|
6 |
14 |
20 |
|
NMHS a2 |
|
16 |
5 |
21 |
|
NMHS business |
|
23 |
2 |
25 |
|
NMHS home arts |
1 |
13 |
|
14 |
|
NMHS vocational |
|
16 |
|
16 |
|
OCHS |
1 |
4 |
1 |
6 |
|
OIHS |
5 |
26 |
|
31 |
|
Our Lady of Mercy VTS |
|
5 |
4 |
9 |
|
PICS |
14 |
221 |
113 |
348 |
|
Pentecostal Lighthouse |
6 |
11 |
4 |
21 |
|
Saramen |
1 |
19 |
25 |
45 |
|
SDA (YAP) |
|
5 |
8 |
13 |
|
SDA PNI |
|
6 |
31 |
37 |
|
SNHS |
24 |
19 |
1 |
44 |
|
SNHS Fefan |
30 |
11 |
3 |
44 |
|
Weno HS |
18 |
34 |
4 |
56 |
|
Xavier HS |
|
|
30 |
30 |
|
Yap HS |
7 |
85 |
43 |
135 |
|
YSC |
|
28 |
10 |
38 |
|
Total Result |
228 |
982 |
404 |
1614 |
Table 4: Program placement by high school
Some schools in the table above provided section level class lists. In recognition that the different high school programs may have different individual goals for their students, this section level data is broken out above. The college thanks the high schools and administrators who have provided this information. Better information from the high schools allows the college to provide more accurate feed back to those schools.
Note that the table above reports the high school name using the names provided to this author by those working on behalf of the admissions board.
The average COMET score seen in table four represents a measure of the relative performance across all sections as weighted by the z-score. High school names are as in the original data, refer to table three above for clarification.
|
School |
COMET |
School |
COMET |
School |
COMET |
|
Xavier HS |
953 |
YSC |
609 |
MCHS |
472 |
|
KHS a1 |
932 |
BEREA |
609 |
PLHA |
465 |
|
SDA PNI |
889 |
NMHS a2 |
600 |
CSC |
459 |
|
CCA PNI |
888 |
NMHS |
582 |
OIHS |
433 |
|
NMHS a1 |
769 |
CSDA |
582 |
WHS |
404 |
|
SDA (YAP) |
741 |
Overall Avg |
552 |
NICHS |
400 |
|
SARAMEN |
717 |
MHS |
548 |
CHS |
400 |
|
KHS a2 |
704 |
KHS non a1,a2 |
535 |
Mortlocks |
323 |
|
OLMVTS |
675 |
NMHS b |
514 |
SNHS |
308 |
|
PICS |
626 |
NMHS h |
507 |
SNHS-F |
297 |
|
YHS |
625 |
NMHS v |
498 |
FHS |
222 |
|
KHS |
616 |
OCHS |
474 |
|
|
Table 5: Average COMET score by high school
A COMET mean below 400 is exceptionally weak and below 300 represents essentially random performance on all included subsections. Two high schools had an average COMET score below certificate admission level. This should be looked upon as an opportunity for improvement.
Bearing in mind that admissions is zero sum, it is not possible for all schools to score above 700. That said, schools or sections with averages above 700 deserve a "well done" for their strong performances.
While the individual high school scores are of interest to individual schools, state educational leadership might consider the mean performance of all of the schools in their state.
Where a performance is strong, no one effort can be credited with the success. Where a performance is weak, no one lack can be faulted as the cause of the poor performance. Education is a set of canoes with many people paddling. Students, parents, teachers, administrators, state leadership, and special programs should all share in the credit where credit is due, in the blame where performances are weak.
Essay section
The writing section is considered by both the language and literature division and by those from other divisions who mark this section to possibly be singularly indicative of the capacity of students to academically succeed at the college – if there is such a thing as a single indicator. The maximum possible score is a fifty. Scores of twenty and under are considered to be significantly weak and raise questions as to whether these students can tackle any program that requires the ability to communicate in written English.
Determining whether one high school is statistically significantly stronger in essay rank order than another high school requires determining whether the mean essays scores are sufficiently separated.
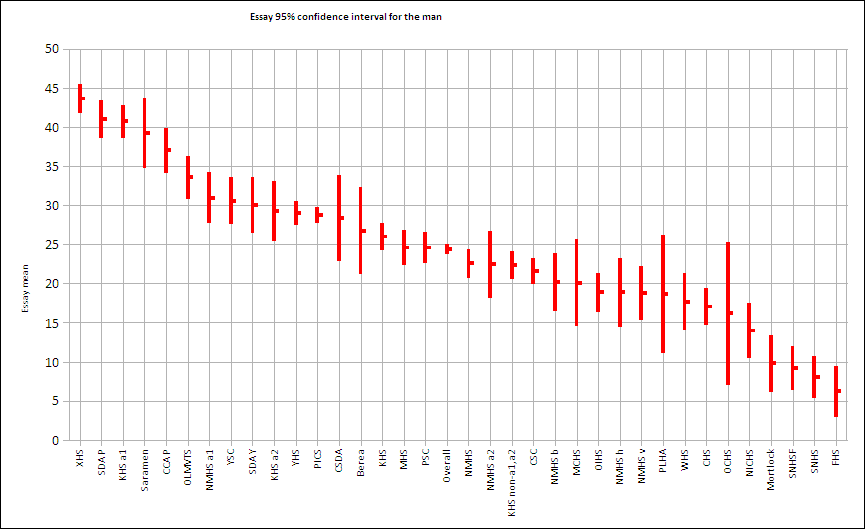
In illustration 2, the vertical bars show the extent of the 95% confidence interval for the mean essay score. Where a bar for one school overlaps the mean for another school, the former is not statistically separated from the mean of the later. The mean is marked by the horizontal line at the midpoint of the vertical bar.
The vertical axis in illustration two is the essay score, the high schools are listed in descending rank order.
Illustration
2: Essay mean by site with 95% confidence interval for the mean
Note that the mean for NMHS is for all sections, while NMHS a1 would be for only the a1 section at NMHS. Splitting out the academic sections is important as it makes more realistic comparisons possible.
The mean essay scores suggest that Kosrae, Pohnpei, and Yap states are, to differing degrees, accomplishing the task of instructing students in the skills necessary to compose written English essays.
Looking at the individual public high schools in Chuuk indicates an almost complete lack of ability to accomplish a written composition in the English language.
An average of 20 is the equivalent result of two essay readers rating the essay as being two in all categories. Averages below 10 would be the result of being awarded a one in all categories. Below 10, the essay has errors of grammar that are so severe as to make comprehension virtually impossible, the vocabulary is limited and misused, and the answer bears little relation to the task set by the essay question. The rubric is included at the end of this report.
While some fields such as science have significant support costs, English language and literature is likely the least expensive program on a per student basis. This is not likely a failure due to a lack of funding alone.
Also of note this year are a couple of new arrival in the list of schools, Our Lady of Mercy Vocational Technical school and Southern Noumeneas High School at Fefan. Our Lady of Mercy has done well for a rookie year.
To be all too blunt, the performance each newer high school in Chuuk casts doubt on the wisdom of splitting out the high school students from Weno back to their home islands in the lagoon. Each newer lagoon high school is weaker than the original high school from which the students had been split out. This is in contrast to Pohnpei where the new high schools perform on par with or better than the original "parent" high school.
Changes in essay performance 2007 to 2008
With the essay marked against the same rubric in 2007 and 2008, year-to-year differences can be determined. Small differences are not statistically significant. With only two years worth of comparable data, the year-to-year variation for any one school cannot be known. If the same rubric is used in spring 2009, then any three-year trends are more likely to be significant than small changes in the mean.
The table is in roughly alphabetic order.
|
Spring 2007 |
Spring 2008 |
|
||
|
HS essay |
mean |
HS essay |
mean |
change |
|
Berea |
15.70 |
BEREA |
26.73 |
11.03 |
|
CCA |
42.00 |
CCA PNI |
39.25 |
-2.75 |
|
CHS |
9.97 |
CHS |
17.04 |
7.07 |
|
CSDA |
20.80 |
CSDA |
28.38 |
7.58 |
|
Faichuk |
4.95 |
FHS |
6.18 |
1.23 |
|
KHS |
26.91 |
KHS |
25.99 |
-0.93 |
|
KHS adv |
37.27 |
KHS a1 |
40.71 |
3.44 |
|
KHS a2 |
38.31 |
KHS a2 |
29.23 |
-9.08 |
|
Mizpah |
21.05 |
MCHS |
20.10 |
-0.95 |
|
Mado HS |
26.36 |
MHS |
24.59 |
-1.77 |
|
NICHS |
19.58 |
NICHS |
13.98 |
-5.61 |
|
NMS |
27.75 |
NMHS |
22.58 |
-5.17 |
|
NMS a |
36.74 |
NMHS a1 |
30.95 |
-5.79 |
|
|
|
NMHS a2 |
22.43 |
|
|
NMS b |
23.74 |
NMHS b |
20.20 |
-3.54 |
|
NMS v1 |
19.00 |
NMHS h |
18.85 |
-0.15 |
|
NMS v2 |
20.91 |
NMHS v |
18.81 |
-2.10 |
|
Nukuno |
12.91 |
|
|
|
|
Ohwa |
23.33 |
OCHS |
16.17 |
-7.17 |
|
OIHS |
21.30 |
OIHS |
18.87 |
-2.43 |
|
|
|
OLMVTS |
33.56 |
|
|
PICS |
25.16 |
PICS |
28.73 |
|
|
PICS a1 |
34.48 |
|
|
|
|
PICS aca |
28.68 |
|
|
|
|
PICS bus |
26.91 |
|
|
|
|
PICS voc |
19.26 |
|
|
|
|
PLHA |
14.69 |
PLHA |
18.67 |
3.98 |
|
PSDA |
37.22 |
SDA PNI |
41 |
3.78 |
|
Saramen |
28.69 |
SARAM |
37 |
8.31 |
|
YSDA |
40.44 |
SDA (YAP) |
30 |
-10.44 |
|
SNHS |
14.05 |
SNHS |
8.02 |
-6.03 |
|
|
|
SNHS-F |
9.18 |
|
|
Weno |
14.81 |
WHS |
17.65 |
2.84 |
|
Xavier |
40.27 |
XHS |
43.63 |
3.36 |
|
YHS |
23.86 |
YHS |
28.99 |
5.14 |
|
Overall |
22.03 |
Overall |
24.35 |
0.21 |
Table 6: Changes in mean essay score 2007 to 2008
Although year-to-year variation in the mean for schools is not know, changes of five or more may prove significant. For example, a study of the actual Saramen essay scores for spring 2007 and spring 2008 indicates that the gain of 8.31 is statistically significant. The drop in score for the NMHS academic sections on the essay is also statistically significant.
Mathematics section
Year-to-year mathematics subsection performance
Table five records the year-to-year performance from 2005 to 2008 on the mathematics subsections. The table also shows the averages for the top four-hundred rank order students on each subsection for 2006, 2007, and 2008
|
95 |
2005 |
4.00 |
|
2006 |
6.69 |
|
|
2007 |
6.63 |
|
|
2008 |
6.83 |
|
|
2006 top 400 |
8.57 |
|
|
2007 top 400 |
8.22 |
|
|
2008 top 400 |
8.27 |
|
|
96 |
2005 |
3.25 |
|
2006 |
3.69 |
|
|
2007 |
4.04 |
|
|
2008 |
4.60 |
|
|
2006 top 400 |
5.74 |
|
|
2007 top 400 |
6.31 |
|
|
2008 top 400 |
6.87 |
|
|
99 |
2005 |
3.08 |
|
2006 |
3.51 |
|
|
2007 |
3.40 |
|
|
2008 |
3.60 |
|
|
2006 top 400 |
5.74 |
|
|
2007 top 400 |
5.45 |
|
|
2008 top 400 |
5.45 |
|
|
100 |
2005 |
2.25 |
|
2006 |
2.43 |
|
|
2007 |
2.49 |
|
|
2008 |
2.55 |
|
|
2006 top 400 |
3.27 |
|
|
2007 top 400 |
3.32 |
|
|
2008 top 400 |
3.41 |
Table 7: Changes in mean math score by math subsection
Year-to-year the averages for each subsection improved slightly for all sections. For the top 400 students the averages improved in three of the four subsections, one subsection remained static. These changes are not individually significant. There is, however, an underlying trend of increasing averages. Those trends are encouraging, although an average of two on a section is no better than random.
Mean Mathematics Scores by High School
The mean score by high school for the mathematics section represents the average number correct out of forty for a high school.
A student blindly guessing on all forty questions, each with five multiple choice options, should get at least eight correct. Given that the first few problems involve basic arithmetic, scores around twelve or under are extremely weak performances.
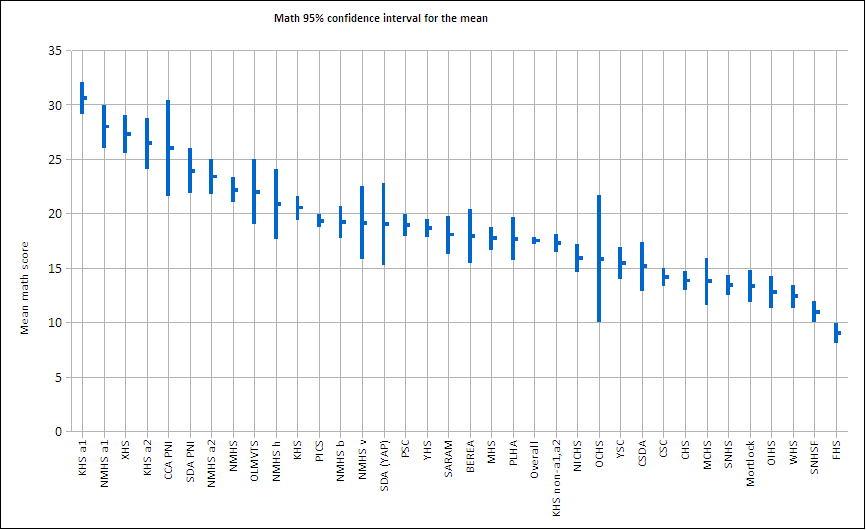
Illustration three on the next page depicts the 95% confidence interval for the mean mathematics scores, with the high schools in descending mathematics score order. The vertical bars are the extent of the 95% confidence interval for the sample mean. Where a vertical line for one school overlaps the mean (the center line) of a another school, the first school is not statistically significantly separated from the second school's mean.
Illustration
3: Mean math sum by high school with 95% confidence intervals
Of note on the chart above are the strong performances by the academic sections at Kosrae High School and Nanpei Memorial High School. The Kosrae High School advanced a1 section was statistically separated from other schools and took first rank.
Nanpei Memorial's a1 section ranked second in the nation, with Xavier rounding out the podium finishes. Also of note is that Kosrae High School's a2 section edged out Calvary Christian Academy. Nanpei Memorial's a2 came in just behind Pohnpei SDA. All of these averages are high and encouraging.
At under 12 were both Southern Noumeneas High School at Fefan and Faichuuk High School. These performances are so close to random that one could effectively argue there would be no significant impact from the cessation of the teaching of mathematics. Shift the resources into language acquisition skills.
Mathematics Placement Data
Placement of students by high school and the program into which they were admitted is shown in the following table.
|
|
NonAdmit |
Certificate |
Associates |
|
||||||||||
|
School |
95 |
96 |
99 |
95 |
96 |
99 |
100 |
101 |
95 |
96 |
99 |
100 |
101 |
Sum |
|
BEREA |
1 |
1 |
|
8 |
7 |
1 |
|
|
2 |
2 |
2 |
1 |
1 |
26 |
|
CCA PNI |
|
|
|
|
1 |
|
|
|
2 |
2 |
|
6 |
1 |
12 |
|
CHS |
33 |
6 |
|
34 |
27 |
6 |
1 |
|
2 |
2 |
2 |
1 |
|
114 |
|
CSC |
12 |
2 |
|
73 |
47 |
3 |
1 |
|
1 |
3 |
1 |
1 |
|
144 |
|
CSDA |
|
|
|
3 |
3 |
|
|
|
1 |
1 |
|
|
|
8 |
|
FHS |
36 |
1 |
|
8 |
|
|
|
|
|
|
|
|
|
45 |
|
KHS non-a1,a2 |
4 |
2 |
|
48 |
26 |
6 |
5 |
|
4 |
8 |
|
2 |
|
105 |
|
KHS a1 |
|
|
|
|
|
|
|
|
|
4 |
1 |
5 |
11 |
21 |
|
KHS a2 |
|
|
|
1 |
4 |
|
4 |
1 |
1 |
2 |
2 |
2 |
5 |
22 |
|
MCHS |
4 |
|
|
8 |
5 |
|
|
|
1 |
1 |
|
1 |
|
20 |
|
MHS |
6 |
1 |
|
27 |
29 |
14 |
3 |
|
1 |
7 |
5 |
7 |
|
100 |
|
Mortlocks |
12 |
1 |
|
10 |
5 |
2 |
|
|
|
|
|
|
|
30 |
|
NICHS |
5 |
5 |
|
9 |
16 |
5 |
|
|
|
1 |
1 |
|
|
42 |
|
NMHS a1 |
|
|
|
|
|
2 |
4 |
|
1 |
1 |
1 |
11 |
|
20 |
|
NMHS a2 |
|
|
|
|
4 |
9 |
3 |
|
|
1 |
3 |
1 |
|
21 |
|
NMHS b |
|
|
|
4 |
15 |
2 |
2 |
|
|
1 |
|
1 |
|
25 |
|
NMHS h |
1 |
|
|
2 |
6 |
3 |
2 |
|
|
|
|
|
|
14 |
|
NMHS v |
|
|
|
2 |
8 |
3 |
3 |
|
|
|
|
|
|
16 |
|
OCHS |
1 |
|
|
3 |
1 |
|
|
|
|
|
1 |
|
|
6 |
|
OIHS |
4 |
1 |
|
16 |
9 |
1 |
|
|
|
|
|
|
|
31 |
|
OLMVTS |
|
|
|
1 |
3 |
1 |
|
|
1 |
|
|
3 |
|
9 |
|
PICS |
12 |
2 |
|
77 |
121 |
15 |
8 |
|
6 |
46 |
19 |
22 |
20 |
348 |
|
PLHA |
3 |
2 |
1 |
4 |
4 |
2 |
1 |
|
|
2 |
2 |
|
|
21 |
|
SARAMEN |
1 |
|
|
8 |
10 |
1 |
|
|
10 |
8 |
3 |
4 |
|
45 |
|
SDA (YAP) |
|
|
|
2 |
2 |
|
1 |
|
2 |
3 |
3 |
|
|
13 |
|
SDA PNI |
|
|
|
1 |
5 |
|
|
|
4 |
6 |
2 |
15 |
4 |
37 |
|
SNHS |
23 |
1 |
|
15 |
4 |
|
|
|
1 |
|
|
|
|
44 |
|
SNHSF |
30 |
|
|
11 |
|
|
|
|
2 |
1 |
|
|
|
44 |
|
WHS |
18 |
|
|
23 |
10 |
1 |
|
|
2 |
1 |
|
1 |
|
56 |
|
XHS |
|
|
|
|
|
|
|
|
5 |
2 |
5 |
17 |
1 |
30 |
|
YHS |
6 |
1 |
|
29 |
40 |
11 |
5 |
|
9 |
16 |
12 |
6 |
|
135 |
|
YSC |
|
|
|
11 |
15 |
1 |
1 |
|
2 |
5 |
2 |
1 |
|
38 |
|
Total Result |
202 |
25 |
1 |
428 |
422 |
87 |
44 |
1 |
60 |
126 |
67 |
108 |
43 |
1614 |
Table 8: Math placement by high school
Diversity
The differences in the performances by state have repercussions on the make-up of the regular admissions. The table below compares the composition of the regular admissions to the state shares of the national population. The table reflects the state of the high school, not the cultural identity of the individual test takers.
|
|
2006 |
2007 |
2008 |
|
|
Factors |
|||||
|
State |
Assoc |
RF |
Assoc |
RF |
Assoc |
RF |
Pop 2000 |
Pop RF |
2006 |
2007 |
2008 |
|
Chuuk |
75 |
18% |
59 |
15% |
93 |
23% |
53595 |
50% |
0.35 |
0.29 |
0.46 |
|
Kosrae |
55 |
13% |
63 |
16% |
47 |
12% |
7686 |
7% |
1.81 |
2.19 |
1.62 |
|
Pohnpei |
225 |
53% |
221 |
55% |
201 |
50% |
34486 |
32% |
1.65 |
1.71 |
1.54 |
|
Yap |
67 |
16% |
57 |
14% |
63 |
16% |
11241 |
11% |
1.51 |
1.36 |
1.48 |
|
|
422 |
100% |
400 |
100% |
404 |
100% |
107008 |
100% |
|
|
|
Table 9: Diversity
Thus in terms of the high school's state share of the national population, students from high schools in Kosrae are the most over-represented group in the regular admissions category with 1.62 times their share of the national population, down from 2.19 the previous year. Those from high schools in Chuuk are under-represented at a factor of 0.46 of their share of the national population, a rise from 0.30 the year before. Each high school has students from every state, however the data is still likely roughly reflective of the underlying cultural diversity of those who took the entrance test.
Note that as one state gains an increasing share of the 400 associate degrees slots, other states lose share. As noted earlier, this is a zero-sum game.
The complication in terms of actual diversity of the freshmen class at the national site is that the differential rates of matriculation into the college are not known. Anecdotally there is the suggestion that Pohnpeians are more likely to take up the offer to attend an associate degree program at Palikir than students in the other states. This may further skew the diversity away from the national share of the population.
Grade Level Equivalents
The vocabulary and comprehension tests permitted the calculation of grade level equivalents
|
Test |
Non-admit |
Certificate |
Associates |
Overall |
|
Vocabulary |
3.47 |
4.28 |
7.00 |
4.85 |
|
Comprehension |
5.54 |
7.25 |
10.74 |
7.89 |
|
Overall |
4.40 |
5.64 |
8.97 |
6.30 |
Table 10: Mean grade level equivalent by admission status
Candidates accepted into associates degree programs have a vocabulary grade level equivalent of seventh grade with a comprehension grade level equivalent of nearly eleventh grade. The certificate program instructors can expect students with a fourth grade equivalent vocabulary level and a seventh grade equivalent comprehension. The non-admitted students are properly non-admitted unless the college wants to start admitting third grade level equivalent students.
The following table provides the vocabulary grade level equivalent for the high schools in descending rank order. Pilot studies have indicated that the college students are weaker in vocabulary than in comprehension. The argument made is that a student can "bridge" across misunderstood vocabulary from context, hence one's comprehension can exceed one's vocabulary.
|
School |
Voc GE |
School |
Voc GE |
School |
Voc GE |
|
XHS |
8.55 |
PICS |
5.09 |
PLHA |
4.27 |
|
CCA PNI |
8.15 |
OCHS |
5.07 |
OIHS |
4.18 |
|
SDA PNI |
7.69 |
YSC |
5.04 |
WHS |
4.09 |
|
SDA (YAP) |
7.38 |
KHS non-a1,a2 |
4.88 |
NICHS |
4.05 |
|
KHS a1 |
7.17 |
Total Result |
4.85 |
CSC |
3.92 |
|
NMHS a1 |
6.22 |
CSDA |
4.84 |
NMHS h |
3.9 |
|
KHS a2 |
5.71 |
PSC |
4.61 |
SNHS |
3.88 |
|
BEREA |
5.65 |
MHS |
4.55 |
Mortlock |
3.85 |
|
YHS |
5.45 |
MCHS |
4.49 |
SNHSF |
3.77 |
|
SARAMEN |
5.41 |
OLMVTS |
4.46 |
CHS |
3.76 |
|
NMHS a2 |
5.1 |
NMHS v |
4.32 |
FHS |
3.09 |
|
|
|
NMHS b |
4.29 |
|
|
Table 11: Vocabulary Grade Level Equivalent by high school
Of interest is the strong performance by the a1 and a2 sections at Kosrae High School and Nanpei Memorial High School. The reality is that the private schools have a larger percentage of students who are likely to have either grown up with English in their home or environment. Private schools such as Pohnpei SDA use English starting in preschool, and some students are from families where one or both parents are L1 speakers of English. That Kosrae High School and Nanpei Memorial can compete is a credit to the students, teachers, administrators, and parents. The only concern might be to ensure that L1 local language skills not be neglected in the push to acquire English.
At the other end of the scale, Faichuuk has used twelve years to produce three years worth of vocabulary learning.
Comprehension grade level equivalents are higher for the schools.
|
School |
Comp GE |
School |
Comp GE |
School |
Comp GE |
|
KHS a1 |
11.91 |
PICS |
8.41 |
MCHS |
7.57 |
|
SDA (YAP) |
11.16 |
OCHS |
8.33 |
PLHA |
6.87 |
|
SDA PNI |
11.00 |
OLMVTS |
8.28 |
NICHS |
6.82 |
|
XHS |
10.95 |
NMHS b |
8.03 |
OIHS |
6.82 |
|
CCA PNI |
10.83 |
NMHS h |
7.98 |
CSC |
6.66 |
|
NMHS a1 |
10.33 |
CSDA |
7.93 |
WHS |
6.45 |
|
KHS a2 |
9.03 |
KHS non-a1,a2 |
7.92 |
CHS |
6.24 |
|
YHS |
8.88 |
Overall |
7.89 |
SNHS |
6.16 |
|
SARAMEN |
8.87 |
YSC |
7.88 |
Mortlocks |
6.06 |
|
NMHS a2 |
8.84 |
NMHS v |
7.87 |
SNHSF |
6.01 |
|
BEREA |
8.51 |
PSC |
7.70 |
FHS |
5.24 |
|
|
|
MHS |
7.64 |
|
|
Table 12: Comprehension grade level equivalent by high school
The top rank performance of the Kosrae High School a1 section is remarkable. The differential of nearly a grade level above other schools is phenomenal. A number of private schools have also turned in impressive results. These students are likely to be able to use their comprehension levels to deal with their vocabulary deficits.
Again, Nanpei Memorial High School a1 has performed strongly. I suspect there might be equally strong performances from PICS a1, but that subgroup was not available to this author.
Arguably the most interesting data is the strong performance by Yap high school. This author's limited understanding of the structure of Yap high school is that there are not separate streams, but rather a common curriculum for all. Yap high school has lifted not a single classroom, but a whole school and again the students, schools, teachers, administrators, parents, and community are all to be commended. The challenge for Yap state appears to be to extend this excellence to Outer Island High School on Ulithi and Neighboring Islands Central High School on Woleai.
The following table reports the number of students at a particular grade level equivalent. The schools are grouped by whether they are a private school or public school, with subgroups by state.
|
Grade Level |
Private |
Public |
|
|||||
|
Equivalent |
Chuuk |
Pohnpei |
Yap |
Chuuk |
Kosrae |
Pohnpei |
Yap |
Sum |
|
2 |
1 |
|
|
6 |
|
|
4 |
12 |
|
4 |
21 |
3 |
|
190 |
25 |
87 |
41 |
433 |
|
6 |
61 |
17 |
3 |
105 |
65 |
302 |
105 |
760 |
|
8 |
25 |
19 |
2 |
10 |
35 |
113 |
40 |
253 |
|
10 |
4 |
8 |
4 |
9 |
16 |
17 |
12 |
72 |
|
12 |
4 |
5 |
3 |
3 |
3 |
13 |
1 |
33 |
|
PHS |
4 |
12 |
1 |
10 |
4 |
12 |
7 |
47 |
|
Totals |
120 |
64 |
13 |
333 |
148 |
544 |
210 |
1614 |
Table 13: Number of students at a grade level equivalent
The grade level equivalents in the above table is based on a combined vocabulary and comprehension score. The data was further binned by even numbered grade levels. The grade level is the bin upper limit. For example, there is one student in a private school in Chuuk with a grade level equivalent (GE) below second grade. Twenty-one students in Chuuk state have a total GE greater than second grade but less than or equal to fourth grade.
Bearing in mind that the mean grade level equivalent for associates admission was 8.97, only the students in the tenth grade bin and higher are above this average. The bulk of the candidates are below this level. Chuuk state public schools in particular have few candidates who function at a level higher than sixth grade.
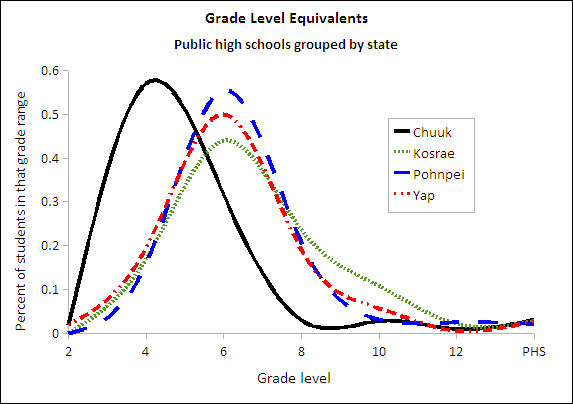
This weakness in Chuuk can be seen more clearly in a relative frequency distribution.
Illustration
4: Relative frequency distribution for Grade level among candidates
from public high schools
Note that the peak of the distribution for Chuuk is to the left of the other three states. While all states could use improvement, Chuuk state is statistically separated from Kosrae, Pohnpei, and Yap states.
TRIO Programs Analysis
The college admissions examination is neither a diagnostic nor comprehensive measure of learning. The college admissions examination is designed for a single purpose: admitting students to the appropriate programs for their abilities in English and mathematics. Despite the focus of the examination, many sponsored programs utilize the admissions results and statistics in their reports. The following are analyses of the essay and mathematics section with some of these subgroups broken out separately.
This author is deeply indebted to those who work in sponsored programs and the high schools who provide lists of student names in programs and sections.
Essay section
The next table details the performance of the TRIO programs.
Many programs use admissions to an associates degree program as a indicator of success. This practice is not recommended. The college admits roughly the top 400 students into associates degree programs as ranked by a z-score using the grammar, essay, and mathematics test. Many of these students will be placed into developmental and not college level programs. Thus admission to an associates degree program is not a statistically meaningful measure. As a result this report does not include admissions status of the subgroups.
The rubric used to mark the essay is provided in an appendix. Two graders mark each essay. If the graders differ by five points, a third grader marks the essay. The college currently considers a score of forty to be a strong essay. Averages of forty or above are exceptionally good results and are likely difficult to improve upon year-to-year.
|
School |
Neither |
TSP |
Upward Bound |
Overall |
|
BEREA |
26.73 |
|
|
26.73 |
|
CCA PNI |
39.25 |
|
|
39.25 |
|
CHS |
13.24 |
|
31.94 |
17.04 |
|
CSC |
21.6 |
|
|
21.6 |
|
CSDA |
28.38 |
|
|
28.38 |
|
FHS |
6.18 |
|
|
6.18 |
|
KHS |
24.22 |
|
35.13 |
25.99 |
|
MCHS |
20.1 |
|
|
20.1 |
|
MHS |
22.65 |
30.88 |
38.25 |
24.59 |
|
NICHS |
13.98 |
|
|
13.98 |
|
NMHS |
20.96 |
24.19 |
30.75 |
22.58 |
|
OCHS |
16.17 |
|
|
16.17 |
|
OIHS |
18.87 |
|
|
18.87 |
|
OLMVTS |
33.56 |
|
|
33.56 |
|
PICS |
27.49 |
32.18 |
41.50 |
28.73 |
|
PLHA |
18.67 |
|
6.33 |
18.67 |
|
SARAM |
37 |
|
|
37 |
|
SDA (YAP) |
30 |
|
|
30 |
|
SDA PNI |
41 |
|
|
41 |
|
SNHS |
8.02 |
|
|
8.02 |
|
SNHSF |
9.18 |
|
|
9.18 |
|
WHS |
17.65 |
|
|
17.65 |
|
XHS |
43.63 |
|
|
43.63 |
|
YHS |
28.32 |
|
35.50 |
28.99 |
|
YSC |
30.58 |
|
|
30.58 |
|
Total Result |
23.64 |
28.97 |
37.09 |
24.35 |
Table 14: TRIO programs essay means
Students in both the Talent Search Program and Upward Bound programs produced higher averages on the essay than students at the same school who were not in a TRIO program with the exception of Upward Bound students at Pentecostal Lighthouse Academy in Chuuk (PLHA). The sample size at PLHA, however, is too small to draw meaningful conclusions.
In 2004 the college experimented with an early run of the entrance test in November. In an attempt to gauge the impact of an early run of the entrance test, nine upward bound juniors in Yap sat for the COMET test. The junior's average was 29.89 on the essay. The juniors were statistically significantly lower than the 35.50 average for the ten upward bound seniors (p-value 0.02). Although significant, results with larger sample sizes from a broader selection of students would still be of interest.
Mathematics Section
The following table details the performance of the high schools in descending mean mathematics score order, repeating an earlier table but including some of the subgroups of interest. The mathematics score is the sum of the four subsections, the total number correct out of forty.
Bear in mind that the the final column of ten problems are set at the level of college algebra, high school students are not expected to succeed at that column. Therefore averages above 26 (80% success in the first three columns of the test and a random two correct in the last column) would be a very strong performance. Lifting a school or a program's average above 30 is likely to be difficult.
|
School |
Neither |
TSP |
Upward Bound |
Overall |
|
BEREA |
17.88 |
|
|
17.88 |
|
CCA PNI |
26 |
|
|
26 |
|
CHS |
12.71 |
|
19.78 |
13.82 |
|
CSC |
14.15 |
|
|
14.15 |
|
CSDA |
15.13 |
|
|
15.13 |
|
FHS |
9 |
|
|
9 |
|
KHS |
18.89 |
|
29.01 |
20.53 |
|
MCHS |
13.75 |
|
|
13.75 |
|
MHS |
16.66 |
20.81 |
26.00 |
17.69 |
|
NICHS |
15.81 |
|
|
15.81 |
|
NMHS |
19.85 |
25.15 |
28.00 |
22.18 |
|
OCHS |
15.83 |
|
|
15.83 |
|
OIHS |
12.76 |
|
|
12.76 |
|
OLMVTS |
21.97 |
|
|
21.97 |
|
PICS |
18.04 |
24.07 |
29.50 |
19.33 |
|
PLHA |
17.78 |
|
17.00 |
17.67 |
|
SARAM |
18.04 |
|
|
18.04 |
|
SDA (YAP) |
19 |
|
|
19 |
|
SDA PNI |
23.92 |
|
|
23.92 |
|
SNHS |
13.41 |
|
|
13.41 |
|
SNHSF |
10.95 |
|
|
10.95 |
|
WHS |
12.37 |
|
|
12.37 |
|
XHS |
27.3 |
|
|
27.3 |
|
YHS |
18.19 |
|
22.80 |
18.64 |
|
YSC |
15.42 |
|
|
15.42 |
|
Total Result |
16.72 |
23.93 |
28.79 |
17.5 |
Table 15: TRIO program math sum averages
Note that on the math section the Yap upward bound juniors had an average of 19.78. On the math section the juniors were not statistically significantly lower than the 22.80 average for the ten upward bound seniors (p-value 0.14). The small sample of juniors performed as well as the seniors on the mathematics entrance test.
Of note is that the TRIO programs in Kosrae and Pohnpei lift public school students to the level of the private schools and above. This provides important opportunities to students in the public school system. This is important to ensure equity in access to a quality college preparatory education. If the only access to a quality education is through private schools, then the nation faces a future where those with the resources potentially generate an intellectual elite that would likely become a governing elite. Down this road lies potential loss of the proverbial "middle class" that seems so crucial to democratic stability and the rise of oligarchic governmental structures.
Programs such as Upward Bound, Talent Search, and others are currently beyond the financial wherewithal of the local governments. Continued United States support for these programs is important to this young nation.
Mathematics Placement Data
The following table shows the break-down of the math placement by TRIO program in four high schools on Kosrae and Pohnpei. In that the mathematics section functions as a placement test, the placement of students has real meaning. There is no "400" limit involved. Theoretically, all students could place into college algebra classes. The class into which students are placed are indicated in the top row.
MS 095 PreAlgebra
MS 096 Elementary Algebra (Algebra I)
MS 099 Intermediate Algebra (Algebra II)
MS 100 College Algebra
MS 101 Algebra and Trigonometry (or MS 150 Statistics)
Students who place into MS 100 or MS 101/101 are deemed college level students for mathematics.
|
School |
Program |
MS 095 |
MS 096 |
MS 099 |
MS 100 |
MS 101 or 150 |
Total |
|
KHS |
None |
56 |
43 |
6 |
13 |
6 |
124 |
|
KHS |
Upward |
2 |
3 |
3 |
5 |
11 |
24 |
|
MHS |
None |
32 |
29 |
15 |
4 |
|
80 |
|
MHS |
TSP |
2 |
6 |
4 |
4 |
|
16 |
|
MHS |
Upward |
|
2 |
|
2 |
|
4 |
|
NMHS |
None |
8 |
27 |
16 |
5 |
|
56 |
|
NMHS |
TSP |
2 |
9 |
6 |
19 |
|
36 |
|
NMHS |
Upward |
|
|
1 |
3 |
|
4 |
|
PICS |
None |
91 |
151 |
25 |
15 |
7 |
289 |
|
PICS |
TSP |
4 |
14 |
8 |
11 |
7 |
44 |
|
PICS |
Upward |
|
4 |
1 |
4 |
7 |
16 |
Table 16: Math placement distribution for TRIO programs in Pohnpei and Kosrae
TRIO programs clearly have a strong positive impact on the math skills of their participants. At a school such as PICS the TRIO programs are responsible for producing over 50% of the students who placed into college level mathematics. At Nanpei Memorial High School 22 of 27 students who are ready for college level math came through a TRIO program. These programs make a difference and are critically important readying students for college.
Author and contact information:
All errors are solely those of the author. Please contact Dana Lee Ling at dleeling@comfsm.fm or 691-320-2480 extension 228 if you have questions, corrections, or unmet data needs in regards the COMET test.
Appendix A.
|
|
COMET Sub-Test 3 (Writing) Analytic Scale [Essay rubric] |
|
|
Syntax |
|
5 |
Grammar and word order nearly perfect. |
|
4 |
Some errors of grammar or word order but communication not impaired. |
|
3 |
Errors of grammar or word order fairly frequent; occasional re-reading necessary for full comprehension. |
|
2 |
Errors of grammar or word order frequent; efforts of interpretation sometimes required on reader’s part. |
|
1 |
Errors of grammar or word order very frequent; reader often has to rely on own interpretation. |
|
0 |
Errors of grammar or word order so severe as to make comprehension virtually impossible. |
|
|
Vocabulary |
|
5 |
Wide and correctly used vocabulary. |
|
4 |
Occasionally uses inappropriate terms or relies on circumlocution; expression of ideas not impaired. |
|
3 |
Uses wrong or inappropriate words fairly frequently; expression of ideas may be limited because of inadequate vocabulary. |
|
2 |
Limited vocabulary and frequent errors clearly hinder expression of ideas. |
|
1 |
Vocabulary so limited and so frequently misused that reader must often rely on own interpretation. |
|
0 |
Vocabulary limitations so extreme as to make comprehension virtually impossible. |
|
|
Organization |
|
5 |
Extremely well organized. |
|
4 |
Material fairly well organized; links could occasionally be clearer but communication not impaired. |
|
3 |
Some lack of organization; re-reading required for clarification of ideas. |
|
2 |
Little or no attempt at connectivity, though reader can deduce some organization. |
|
1 |
Individual ideas may be clear, but very difficult to deduce connection between them. |
|
0 |
Lack of organization so severe that communication is seriously impaired. |
|
|
Cohesion |
|
5 |
Strong cohesion with smooth transitions both within and between paragraphs. |
|
4 |
Occasional lack of consistency in choice of cohesive structures and vocabulary but overall ease of communication not impaired. |
|
3 |
‘Patchy’, with some cohesive structures or vocabulary items noticeably inappropriate to general style. |
|
2 |
Cohesive structures or vocabulary items sometimes not only inappropriate but also misused; little sense of ease of communication. |
|
1 |
Communication often impaired by completely inappropriate or misused cohesive structures or vocabulary items. |
|
0 |
A ‘hotchpotch’ of half-learned misused cohesive structures and vocabulary items rendering communication almost impossible. |
|
|
Content |
|
5 |
Full and complete answer, inclusive of all parts of the task. |
|
4 |
Relevant and adequate answer to the task set. |
|
3 |
For the most part answers the task set, though there may be some gaps or redundant information. |
|
2 |
Answer of limited relevance to the task set. Possibly major gaps in treatment of topic and/or pointless repetition. |
|
1 |
Answer bears little relation to the task set. |
|
0 |
No evidence of assigned task. (If it is obvious that the student wrote on an unrelated topic or did not understand the instructions, give zeros in all areas.) |